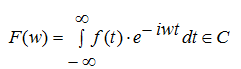Transformata fourier și transformata Fourier Digitală
Definitie și formulă matematică
iar fk
se numeşte eşantionul spectrului lui x pe frecvenţa k
Digital fourier transformation - DFT:
Modul de calcul al spectrului unui
semnal in timp discret x[n], n=0,…,N-1,
se bazează pe utilizarea funcţiilor sin
si cos din biblioteca matematică a
limbajului C. După ce se aplică formulele prezentate mai jos rezultatul este o mărime complexă, z.
Ceea ce ne interesează în cazul analizei de frecvență a unui semnal digital este modulul acestui număr complex, având semnificaţia fizica de amplitudine a semnalului la diferite frecvenţe, practic ne interesează doar P[k].
Practic eu am decupat semnalul sonor folosind o fereastră de tip Hamming, și am calculat spectrul de frecvență pe această bucățică din semnal. Apoi am deplasat fereastra cu câteva sample-uri la dreapta și am repetat procesul:
Rezultatul analizei de frecvență pentru un singur cuvânt:
Implementare
Clasa DFT_Spectrum de mai jos contine pe lângă metoda de determinare a spectrului (dft) și toate metodele pentru decupare a semnalului acustic, MelScale , convolutie și filtrare :
//------------------------clasa pentru DSP analiza spectrala si compresie-------
class DFT_Spectrum
{
public:
double s[1024];
Complex spec[1024];
double mels[1024];
double cep[1024];
double filtreTriunghiulare[1024][16];
double mas;
double esantioane[80000];
double Window[3000];
double WindowS[1024];
double Convolutia[3000];
//-----------metodele--------------------------------------------
void dft(int ns)
{
double suma_real=0,suma_imag=0,Magnitudine;
int h=0,k=0,j=0;
double re,im;
double c1,c2;
c1=2.0*M_PI/double(ns);
c2=2.0/double(ns);
Complex z;
h=0;
for (k=0; k<ns/2; k++)
{
h++;
suma_real = 0;
suma_imag = 0;
for(j=0; j<ns; j++)
{
suma_real += double(esantioane[j])*cos(double(k)*double(j)*c1);
suma_imag += double(esantioane[j])*sin(double(k)*double(j)*c1);
}
spec[h].real =c2*double(suma_real);
spec[h].imaginar=c2*double(suma_imag);
Magnitudine =z.modul(spec[h]);
s[h] =20.0*log10(1+Magnitudine);
}
}
//-------------------------------------------------------------
void SetEsant_Double(double Esant[80000],int nr)
{
for(int i=0; i<nr; i++)
{
esantioane[i]=Esant[i];
}
}
//--------------------------------------------------------------
void DCT(int ns)
{
static double suma=0;
static int h=0,k=0,j=0;
static double c1;
c1= M_PI/double(ns);
h=0;
for(k=0; k<1024; k++)
{
h++;
suma = 0;
for(j=0; j<ns; j++)
{
suma+= mels[j]*cos((double(k)-0.5)*double(j)*c1);
}
cep[h]=suma;
}
}
//-------------------------------------------------------------
void Logaritmare(int n)
{
for(int i=0; i<n; i++)
{
mels[i]=20.0*log10(1 + s[i]);
}
}
//-------------------------------------------------------------
void GenHamming(int wn)
{
for(int i=0; i<wn-1; i++)
Window[i]=0.54-0.46*cos(2.0*double(i)*1.0/wn*M_PI);
}
//------------------------------------------------------------
void GenRandomSpectrum()
{
randomize();
for(int i=0; i<1024; i++)
s[i]=random(1000)/100.0;
}
//-------------------------------------------------------------
void GenBlackman(int wn)
{
for(int i=0; i<wn-1; i++)
Window[i]=0.35875-0.48829*cos(2.0*double(i)*1.0/wn*M_PI)
+0.14128*cos(4.0*double(i)*1.0/wn*M_PI)
-0.01168*cos(6.0*double(i)*1.0/wn*M_PI);
}
//-------------------------------------------------------------
void GenHann(int wn)
{
for(int i=0; i<wn-1; i++)
Window[i]=0.5*(1-cos(2.0*double(i)*1.0/wn*M_PI));
}
//-------------------------------------------------------------
void GenXHann(int wn)
{
for(int i=0; i<wn-1; i++)
{
if(i<=wn/4-1)
Window[i]=0.5*(1-cos(2.0*double(i)*1.0/(wn/2)*M_PI));
else
{
if((i>=wn/4)&&(i<=3*wn/4-1))
Window[i]=1.0;
if(i>=3*wn/4)
Window[i]=0.5*(1-cos(2.0*double(i)*1.0/(wn/2)*M_PI));
}
}
}
//------------------------------------------------------------
void GenRect(int wn)
{
for(int i=0; i<wn-1; i++)
Window[i]=1.0;
}
//-------------------------------------------------------------
void GenTriunghi(int wn)
{
int h=0;
for(int i=0; i<wn-1; i++)
if(i<wn/2)
{
Window[i]=double(i)/double(wn);
h++;
}
else
{
Window[i]=double(h)/double(wn);
h--;
}
}
//------------------------------------------------------------------
void GenFiltreTriungiulare(int wn)
{
int h=1,lungime=0,nrFer=0,a32=0,depl=wn;
wn=1;
a32=0;
do
{
h=1;
if(nrFer==0)
{
for(int i=1; i<=depl; i++)
{
filtreTriunghiulare[i][nrFer]=1.0;
}
a32=depl;
}
else
{
wn=wn*2;
for(int i=1; i<=wn; i++)
{
if(i<wn/2)
{
filtreTriunghiulare[i+a32][nrFer]=double(i)/double(wn);
h++;
}
else
{
filtreTriunghiulare[i+a32][nrFer]=double(h)/double(wn);
h--;
}
}
}
if(nrFer==0)
{
a32=depl;
nrFer++;
}
else
{
nrFer++;
a32=wn+depl;
}
}
while(nrFer<11);
}
//-------------------------------------------------------------
void FiltruTriunghiular(int nrFiltru)
{
for(int i=0; i<512; i++)
{
WindowS[i] = s[i]* filtreTriunghiulare[i][nrFiltru];
}
}
//-------------------------------------------------------------
void BubbleSort()
{
double aux=0.0;
bool gata;
do
{
gata=true;
for(int i=1; i<1024; i++)
if(WindowS[i+1]>WindowS[i])
{
aux=WindowS[i+1];
WindowS[i+1]=WindowS[i];
WindowS[i]=aux;
gata=false;
}
}
while(gata!=true);
}
//-------------------------------------------------------------
void Convolutie(int n,int indx)
{
static double s=0;
static double tau=0;
static double tx=0;
for(int tau=0; tau<(n-1); tau++)
{
s=0;
for(int i=0; i<(n-1); i++)
{
tx=tau-i;
if(tx<0)
{
tx=tx+n;
}
s+=esantioane[i+indx]*Window[i];
}
Convolutia[tau]=s;
}
}
//-------------------------------------------------------------
void PseudoConvolutie(int n,int indx)
{
for(int i=0; i<n-1; i++)
{
Convolutia[i]=0;
Convolutia[i]=esantioane[i+indx]*Window[i];
}
}
//-------------------------------------------------------------
void SumConvolutie(int n,int indx)
{
for(int i=0; i<(n-1); i++)
{
Convolutia[i]=esantioane[i+indx]+Window[i];
}
}
//-------------------------------------------------------------
int getMelscale(int numar)
{
//-------compresia MelScale-----
double nr_frecv=2,suma=0,frecventa_prag=1;
int j=0,index=1,indexp=0,h=0;
//am 512 frecvente
do
{
if(frecventa_prag>1000)
nr_frecv=8;
suma=0;
for(int i=1; i<=nr_frecv; i=i+1)
{
suma+=s[i+j+int(nr_frecv)]; //suma a n frecvente
index=(i+j)/nr_frecv;
}
mels[index]=suma/nr_frecv; //media aritmetica a n frecvente
j=j+nr_frecv;
frecventa_prag = frecventa_prag + 8000.0/(numar);
}
while(j<numar/2);
return index;
}
}; Documentație
- https://ro.wikipedia.org/wiki/Transformata_Fourier
- https://en.wikipedia.org/wiki/Fast_Fourier_transform
An nou fericit !
Pentru întrebari și/sau consultanță tehnică vă stau la dispozitie pe blog sau pe email simedruflorin@automatic-house.ro.
O seară/zi plăcută tuturor !